2020-10-15

Leetcode

Instroduction In order to summarize the algorithm of Leetcode encountered

DP

1626. Best Team With No Conflicts

Question description
1626. Best Team With No ConflictsYou are the manager of a basketball team. For the upcoming tournament, you want to choose the team with the highest overall score. The score of the team is the sum of scores of all the players in the team.

However, the basketball team is not allowed to have conflicts. A conflict exists if a younger player has a strictly higher score than an older player. A conflict does not occur between players of the same age.

Given two lists, scores and ages, where each scores[i] and ages[i] represents the score and age of the ith player, respectively, return the highest overall score of all possible basketball teams.

Example 1

Input: scores = [1,3,5,10,15], ages = [1,2,3,4,5]
Output: 34(choose all)
Example 2

Input: scores = [4,5,6,5], ages = [2,1,2,1]
Output: 16(last 3)
Example 3

Input: scores = [1,2,3,5], ages = [8,9,10,1]
Output: 6(first 3)
Constraints:

1 <= scores.length, ages.length <= 1000
scores.length == ages.length
1 <= scores[i] <= 10⁶
1 <= ages[i] <= 1000

Code & Explanation

Idea is to first sort the players by their age so that we don’t have to always check both the scores and the age to see whether these two players can be in the same team.

We sort age(first) and score(second) in the ascending/descending order
Now we know that for any player i, we can choose any player from 0 to i-1 as long as that player has higher score than this i-th player.

dp[i] stores the maximum score that can be obtained when i-th player is included and all other players are between indices 0 and i-1.
Once we get the answer for all indices, we can simply find the max and that will be the answer.

class Solution {
    class People {
        int age;
        int score;
        public People(int age, int score) {
            this.age = age;
            this.score = score;
        }
    }
    public int bestTeamScore(int[] scores, int[] ages) {
        if (scores == null || ages == null || scores.length != ages.length) return -1;
        
        int n = scores.length;
        People[] people = new People[n];
        for (int i = 0; i < n; i++) {
            people[i] = new People(ages[i], scores[i]);
        }
        
        Arrays.sort(people, (a, b) -> (a.age != b.age ? a.age - b.age : a.score - b.score));
        
        
        int[] dp = new int[n];
        dp[0] = people[0].score;
        int res = dp[0];
        
        for (int i = 1; i < n; i++) {
            dp[i] = people[i].score;
            for (int j = 0; j < i; j++) {
                if (people[j].age == people[i].age || people[j].score <= people[i].score) {
                    dp[i] = Math.max(dp[i], dp[j] + people[i].score);
                }
            }
            res = Math.max(dp[i], res);
        }
        
        return res;
        

    }
}

Complexity

Time: O(n²)
Space: O(n)

1641. Count Sorted Vowel Strings

Question description
Given an integer n, return the number of strings of length n that consist only of vowels (a, e, i, o, u) and are lexicographically sorted.
A string s is lexicographically sorted if for all valid i, s[i] is the same as or comes before s[i+1] in the alphabet.

Example 1

Input: n = 1
Output: 1

Explanation: The 5 sorted strings that consist of vowels only are [“a”,”e”,”i”,”o”,”u”].
Example 2

Input: n = 2
Output: 15

Explanation: The 15 sorted strings that consist of vowels only are
[“aa”,”ae”,”ai”,”ao”,”au”,”ee”,”ei”,”eo”,”eu”,”ii”,”io”,”iu”,”oo”,”ou”,”uu”].
Note that “ea” is not a valid string since ‘e’ comes after ‘a’ in the alphabet.
Example 3

Input: n = 33

Output: 66045
Constraints:

1 <= n <= 50

Code & Explanation

j = 1 only have a
j = 2 only have a,e
j = 3 only have a,e,i
j = 4 only have a,e,i,o
j = 5 only have a,e,i,o,u

_i\^j	1	2	3	4	5
0	1	1	1	1	1
1	1	2	3	4	5
2	1	3	6	10	15
3	1	4	10	20	35
4	1	5	15	35	70
5	1	6	21	56	126

class Solution {
    public int countVowelStrings(int n) {
        
        // tradition dp
        // int[][] dp = new int[n + 1][6];
        // Arrays.fill(dp[0], 1);
        // for (int i = 1; i <= n; i++) {
        //     for (int j = 1; j < 6; j++) {
        //         dp[i][j] = j == 1 ? 1 : dp[i][j-1] + dp[i-1][j];
        //     }
        // }
        // return dp[n][5];
        
        
        // reduce space complexity
        int[] dp = new int[6];
        for (int i = 1; i < 6; i++) dp[i] = 1;
        
        for (int k = 1; k <= n; k++) {
            for (int i = 1; i < 6; i++) {
                dp[i] += dp[i-1];
            }
        }
        
        
        return dp[5];
    }
    /*
    1 a e i o u
    2 aa ae ai ao au, ee ei eo eu, ii io iu, oo ou, uu
    3 aaa aae aai aao aau, aee aei aeo aeu, aii aio aiu, aoo aou, auu; eee eei eeo eeu, eii eio eu, eoo eou, euu;
    iii iio iiu, ioo iou, iuu; ooo oou, ouu; uuu
    */
}

Complexity

Time: O(nk)
Space: O(k)

Solution 2: Combination number
Now we have n characters, we are going to insert 4 l inside.
We can add in the front, in the middle and in the end.
How many ways do we have?
For the 1st l, we have n+1 position to insert.
For the 2nd l, we have n+2 position to insert.
For the 3rd l, we have n+3 position to insert.
For the 4th l, we have n+4 position to insert.
Also 4 l are the same,
there are (n + 1) * (n + 2) * (n + 3) * (n + 4) / 4! ways.

The character before the 1st l, we set to a.
The character before the 2nd l, we set to e.
The character before the 3rd l, we set to i.
The character before the 4th l, we set to o.
The character before the 5th l, we set to u.

We get the one result for the oringinal problem.

public int countVowelStrings(int n) {
        return (n + 1) * (n + 2) * (n + 3) * (n + 4) / 24;
}

Complexity

Time: O(1)
Space: O(1)

Union Find

1627. Graph Connectivity With Threshold

Question description

1627. Graph Connectivity With Threshold We have n cities labeled from 1 to n. Two different cities with labels x and y are directly connected by a bidirectional road if and only if x and y share a common divisor strictly greater than some threshold. More formally, cities with labels x and y have a road between them if there exists an integer z such that all of the following are true:

x % z == 0,
y % z == 0, and
z > threshold.

Given the two integers, n and threshold, and an array of queries, you must determine for each queries[i] = [a_i, b_i] if cities a_i and b_i are connected (i.e. there is some path between them).

Return an array answer, where answer.length == queries.length and answer[i] is true if for the i^th query, there is a path between a_i and b_i, or answer[i] is false if there is no path.

Example 1

Input: n = 6, threshold = 2, queries = [[1,4],[2,5],[3,6]]
Output: [false,false,true]

Explanation: The divisors for each number:
1: 1
2: 1, 2
3: 1, 3
4: 1, 2, 4
5: 1, 5
6: 1, 2, 3, 6
Using the underlined divisors above the threshold, only cities 3 and 6 share a common divisor, so they are the
only ones directly connected.The result of each query:
[1,4] 1 is not connected to 4
[2,5] 2 is not connected to 5
[3,6] 3 is connected to 6 through path 3–6
Example 2

Input: n = 6, threshold = 0, queries = [[4,5],[3,4],[3,2],[2,6],[1,3]]
Output: [true,true,true,true,true]
Explanation: The divisors for each number are the same as the previous example. However, since the threshold is 0
all divisors can be used. Since all numbers share 1 as a divisor, all cities are connected.
Example 3

n = 5, threshold = 1, queries = [[4,5],[4,5],[3,2],[2,3],[3,4]]
Output: [false,false,false,false,false]
Explanation: Only cities 2 and 4 share a common divisor 2 which is strictly greater than the threshold 1, so they are the only ones directly connected.
Please notice that there can be multiple queries for the same pair of nodes [x, y], and that the query [x, y] is equivalent to the query [y, x].
Constraints:

2 <= n <= 10⁴
0 <= threshold <= n
1 <= queries.length <= 10⁵
queries[i].length == 2
1 <= a_i, b_i <= cities
a_i != b_i

Code & Explanation

Because the input sizes are fairly large, we must have close to constant time performance.
One can solve this problem by constructing a graph and then performing DFS for each query,
but it would quickly lead to TLE.

Idea here is to use union find data structure because all we care about is whether there
is exist an edge between a and b. If union-find finds that both a and b belong to the same
component, then there is an edge between them.

Now for union-find to do this, we will first setup the graph. Key idea to understand is that
any integer node a will be connected to all the multiples of a provided that a is greater than
the threshold. For each number from 1 to n, we will connect it to its multiples and then keep
queryin this awesome data structure.

Code should help you realize how easy all this is.

class Solution {
    class UF {
        int distinct;
        int[] roots;
        int[] size;

    public UF(int n) {
        this.distinct = n;
        this.roots = new int[n + 1];
        this.size = new int[n + 1];

        for (int i = 1; i <= n; i++) {
            this.roots[i] = i;
            this.size[i] = 1;
        }
    }


    private int findRoot(int n) {
        if (this.roots[n] == n) return n;

        return this.roots[n] = findRoot(this.roots[n]);
    }

    private void unite(int x, int y) {
        int root_x = findRoot(x);
        int root_y = findRoot(y);
        if (root_x == root_y) return;

        // if (size[x] > size[y]) {
        //     size[x] += size[y];
        //     this.roots[root_y] = root_x;
        // } else {
        //     size[y] += size[x];
        //     this.roots[root_x] = root_y;
        // }
        if (root_x < root_y) {

            this.roots[root_y] = root_x;
        } else {

            this.roots[root_x] = root_y;
        }

        this.distinct--;
    }

    private boolean connect(int i, int j) {
        return findRoot(i) == findRoot(j);
    }

    private boolean united() {
        return this.distinct == 1;
    }
}
public List<Boolean> areConnected(int n, int threshold, int[][] queries) {
    List<Boolean> res = new ArrayList();
    if (threshold == 0) {
        for (int i = 0; i < queries.length; i++) res.add(true);
        return res;
    }
    UF uf = new UF(n);
    // the connected number must bigger than threshold
    for (int i = threshold + 1; i <= n; i++) {
        for (int j = i * 2; j <= n; j += i) {
            uf.unite(i, j);
        }
    }

    for (int[] query : queries) {
        res.add(uf.connect(query[0], query[1]));
    }
    return res;
}
}

Complexity

Time: O(n * log(n)) build union find
Space: O(n)

Tricky

GrayCode

1611. Minimum One Bit Operations to Make Integers Zero

Question description

1611. Minimum One Bit Operations to Make Integers Zero
Given an integer n, you must transform it into 0 using the following operations any number of times:

Change the rightmost (0th) bit in the binary representation of n.
Change the ith bit in the binary representation of n if the (i-1)th bit is set to 1 and the (i-2)th through 0th bits are set to 0.
Return the minimum number of operations to transform n into 0.
Example 1

Input: n = 0
Output: 0
Example 2

Input: n = 3
Output: 2
Explanation: The binary representation of 3 is “11”.
“11” -> “01” with the 2nd operation since the 0th bit is 1.
“01” -> “00” with the 1st operation.
Example 3

Input: n = 6
Output: 4
Explanation: The binary representation of 6 is “110”.
“110” -> “010” with the 2nd operation since the 1st bit is 1 and 0th through 0th bits are 0.
“010” -> “011” with the 1st operation.
“011” -> “001” with the 2nd operation since the 0th bit is 1.
“001” -> “000” with the 1st operation.
Example 4

Input: n = 9
Output: 14
Example 5

Input: n = 333
Output: 393
Constraints:

0 <= n <= 10⁹

Code & Explanation

GrayCode always has the least number of bit changes, so treating the given number as grey code and converting it to decimal gives the correct answer.

Decimal	Binary	GrayCode
0	0000	0000
1	0001	0001
2	0010	0011
3	0011	0010
4	0100	0110
5	0101	0111
6	0110	0101
7	0111	0100
8	1000	1100
9	1001	1101
10	1010	1111
11	1011	1110
12	1100	1010
13	1101	1011
14	1110	1001
15	1111	1000

decimal to graycode
fix the first digit, xor from left to right
1101 => 1 (the first digit is fixed) => 10 (since the first two digit is same) => 101 (since the second digit is different with the third digit) => 1011 (the last two digit is different)

graycode to decimal
fix the first digit, decode from left to right
1011 => 1 (fix the first digit) => 11 (the second is 0, so still is 1) => 110 (the third is 1, so change from 1 to 0) => 1101 (the last is 1, so change from 0 to 1)

class Solution {
   public int minimumOneBitOperations(int n) {
       //graycode to decimal
       int res = 0;
       while (n != 0) {
           res ^= n;
           n >>= 1;
       }
       
       return res;
   }
}
/*
Input 9 Expect output 14

init  
n = 9 = 1001  
res = 0  
loop 1
res ^= n => res = 0000 ^ 1001 = 1001
n >> 1 => n = 100
loop 2  
res ^= n => res = 1001 ^ 100 = 1101  
n >> 1 => n = 10  
loop 3  
res ^= n => res = 1101 ^ 10 = 1111  
n >> 1 => n = 1  
loop 4  
res ^= n => res = 1111 ^ 1 = 1110
n >> 1 => n = 0  
end 
return res = 14
*/

Complexity

Time: O(n.bit.length)
Space: O(1)

BitMask

1617. Count Subtrees With Max Distance Between Cities

Question description

1617. Count Subtrees With Max Distance Between Cities
There are n cities numbered from 1 to n. You are given an array edges of size n-1, where edges[i] = [ui, vi] represents a bidirectional edge between cities ui and vi. There exists a unique path between each pair of cities. In other words, the cities form a tree.

A subtree is a subset of cities where every city is reachable from every other city in the subset, where the path between each pair passes through only the cities from the subset. Two subtrees are different if there is a city in one subtree that is not present in the other.

For each d from 1 to n-1, find the number of subtrees in which the maximum distance between any two cities in the subtree is equal to d.

Return an array of size n-1 where the dth element (1-indexed) is the number of subtrees in which the maximum distance between any two cities is equal to d.

Notice that the distance between the two cities is the number of edges in the path between them.

Example 1

Input: n = 4, edges = [[1,2],[2,3],[2,4]]
Output: [3,4,0]
Explanation:
The subtrees with subsets {1,2}, {2,3} and {2,4} have a max distance of 1.
The subtrees with subsets {1,2,3}, {1,2,4}, {2,3,4} and {1,2,3,4} have a max distance of 2.
No subtree has two nodes where the max distance between them is 3.
Example 2

Input: n = 2, edges = [[1,2]]
Output: [1]
Example 3

Input: n = 3, edges = [[1,2],[2,3]]
Output: [2,1]
Constraints:

2 <= n <= 15(the biggest n is 15 indicates that time complexity should related to 2ⁿ)
edges.length == n-1
edges[i].length == 2
1 <= u_i, v_i <= n
All pairs (u_i, v_i) are distinct.

Code & Explanation

Try every pair of n cities.
From example 1, n = 4, edges = [[1,2],[2,3],[2,4]]
we use bit mast to represemt where it is in this pair.
0000(all absence)
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111(all in)

class Solution {
    public int[] countSubgraphsForEachDiameter(int n, int[][] edges) {
        int[][] dist = new int[n][n];
        List<Integer>[] neighbor = new List[n];
        for (int i = 0; i < n; i++) neighbor[i] = new ArrayList();
        for (int[] edge : edges) {
            neighbor[edge[0] - 1].add(edge[1] - 1);
            neighbor[edge[1] - 1].add(edge[0] - 1);
        }
        
        // use DFS to build a graph, and record distance between each nodes
        for (int i = 0; i < n; i++)
            callDFS(dist, neighbor, i, -1, i, 0);
        
        int[] res = new int[n-1];
        // i from 1 to (1<<n), loop every pair, n = 4, (1 << n) = 16, i = [1, 16), no 0 is because every pari can not be empty 
        for (int i = 1; i < (1 << n); i++) {
            int adjacent = 0;
            int cities = 0;
            int maxDist = 0;
            
            for (int j = 0; j < n; j++) {
            // check if this node in this pair
                if ((i & (1 << j)) != 0) {
                    cities ++;
                    
                    for (int k = j + 1; k < n; k++) {
                    // check if this node int this pair
                        if ((i & (1 << k)) != 0) {
                        // record the maxDist in this pair
                            maxDist = Math.max(maxDist, dist[j][k]);
                            // record how many direct line in this pair
                            if (dist[j][k] == 1) adjacent++;
                        }
                    }
                }
            }
            // check this graph is valid
            if (cities == adjacent + 1 && maxDist > 0) res[maxDist - 1]++;
        }
        
        
        
        return res;
    }
    
    
    private void callDFS(int[][] dist, List<Integer>[] neighbor, int root, int pre, int cur, int curDist) {
        if (pre == cur) return;
        
        dist[root][cur] = curDist;
        dist[cur][root] = curDist;
        
        for (int neighbo : neighbor[cur]) {
            if (neighbo != pre) {
                callDFS(dist, neighbor, root, cur, neighbo, curDist+1);
            }
        }
    }
    }

Complexity

Time: O(2ⁿ * n * n)
Space: O(n²)

Special Data Structure

Binary Indexed Tree

Leetcode 1649

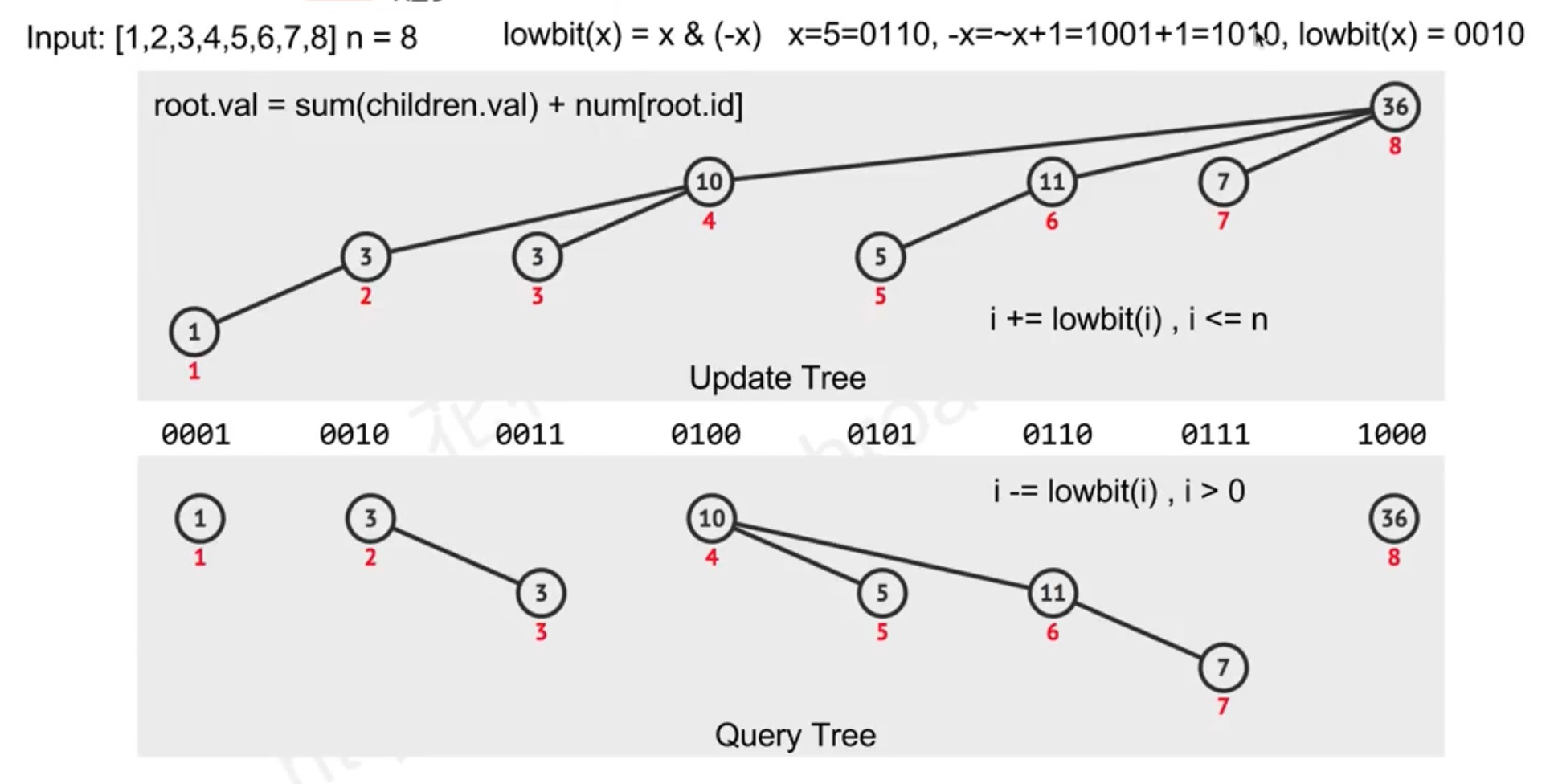
Instruction

coding implement

int n = input.length;
int[] bits = new int[n];
private void update(int idx, int delta) {
    while (idx <= bits.length) {
        bits[idx]+= delta;
        idx += (idx & -idx);
    }
}


private int get(int delta) {
    int res = 0;
    while (delta > 0) {
        res += bits[delta];
        delta -= (delta & -delta);
    }

    return res;
}

SeagmentTree

Leetcode 307

coding implement

class SeagmentTree {
    SeagmentTree left;
    SeagmentTree right;
    int val;
    int start;
    int end;
    public SeagmentTree(int val, int start, int end){
        this.val = val;
        this.start = start;
        this.end = end;
    }
}
SeagmentTree root;
public NumArray(int[] nums) {
    root = buildTree(nums, 0, nums.length - 1);
}

private SeagmentTree buildTree(int[] nums, int start, int end) {
    if (start > end) return null;
    SeagmentTree root = new SeagmentTree(nums[start], start, end);
    if (start != end)  {
        int mid = start + (end - start) / 2;
        root.left = buildTree(nums, start, mid);
        root.right =  buildTree(nums, mid + 1, end);
        root.val = root.left.val + root.right.val;
    }

    return root;
}

public void update(int i, int val) {
    updateSub(root, i, val);
}

private void updateSub(SeagmentTree root, int idx, int val) {
    if (idx < root.start || idx > root.end) return;
    int a = root.start, b = root.end;
    if (root.start == idx && root.end == idx) root.val = val;
    else {
         int mid = root.start + (root.end - root.start) / 2;
        if (idx <= mid) updateSub(root.left, idx, val);
        else {
            updateSub(root.right, idx, val);
        }
        root.val = root.left.val + root.right.val;
    }


}

Title:Leetcode

Author:

Created:2020-10-15, 08:56:11

Updated:2020-12-14, 18:12:23

Full URL:http://example.com/2020/10/15/Leetcode/

License: "CC BY-NC-SA 4.0" Keep Link & Author if Distribute.